Licht [1]
[151] Licht, die Ursache derjenigen Reize unsers Sehorgans, durch welche uns die Außenwelt sichtbar wird.
I. Allgemeines.
Nach der älteren, besonders durch Newton (Optik vom Jahr 1698) vertretenen Hypothese, der Emissionstheorie (Emanationstheorie, Korpuskulartheorie) werden von den leuchtenden Körpern kleine Partikel eines Lichtstoffes ausgeworfen, die alle mit gleicher, in demselben Mittel konstanter Geschwindigkeit den Raum durcheilen, im Auge die Lichtempfindung erregen, an der Oberfläche und im Innern der Körper die mannigfaltigsten optischen Wirkungen erleiden und erzeugen. Die Hypothese ist gescheitert an ihrer Unfähigkeit, die Verminderung der Fortpflanzungsgeschwindigkeit des Lichts beim Uebergang von den optisch dünneren in die optisch dichteren Mittel, ferner die Erscheinungen der Polarisation und der Doppelbrechung und besonders die Erscheinungen der Interferenz zu erklären.
Nach der Undulationstheorie (Wellentheorie, Vibrationstheorie) besteht das Licht in Wellen des Lichtäthers, welcher sowohl den Weltraum, als auch den Raum der Körper, wenigstens der durchsichtigen, durchdringt. Die erste Annahme der Begründer der Undulationstheorie läßt die Aetherwellen in elastischen Schwingungen des Lichtäthers bestehen, der sich als vollkommen unzusammendrückbare Substanz verhalte und daher nur Transversalschwingungen zulasse, keine Longitudinalschwingungen, die durch die Erscheinungen der Polarisation ausgeschlossen zu sein scheinen.
Diese Anschauung ist jetzt durch die elektromagnetische Lichttheorie ersetzt, nach welcher die Aetherwellen in periodischen, sich nach dem Gesetze der Induktion fortpflanzenden elektrischen und zu diesen senkrecht gerichteten magnetischen Schwingungen bestehen. Die Fortpflanzungsgeschwindigkeit aller Aetherwellen ist im leeren Raum = 300000 km in der Sekunde,[151] in den lichtbrechenden Mitteln aber kleiner, je nach deren Substanz und Dichte und je nach der Wellenlänge des Lichts. Nur diejenigen Aetherwellen sind Lichtwellen, d.h. vermögen den menschlichen Sehnerv zur Lichtempfindung zu reizen, deren sekundliche Schwingungszahl zwischen etwa 400 und 770 Billionen oder zwischen den Wellenlängen 760 und 390 Milliontel Millimeter liegt, dem Gebiet des sichtbaren Teils des Spektrums (s. Spektralanalyse).
Aus der Geschichte unsrer Kenntnisse von der Natur und den Gesetzen des Lichts heben wir folgendes heraus: Die Erfindung des Fernrohrs (ca. 1600), die prismatische Zerlegung des Lichts durch Kepler [1], die Entdeckung des Sinusgesetzes der Brechung durch Snellius und durch Descartes [2], die Beschreibung und erste Erklärung der Beugungserscheinungen durch Grimaldi (1650), Olaf Römers Bestimmung der Fortpflanzungsgeschwindigkeit des Lichts aus der Verfrühung oder Verspätung der Verfinsterungen der Jupitertrabanten je nach dem Abstande von Erde und Jupiter (1675), die Begründung der Wellentheorie des Lichts auf die Tatsache der Doppelbrechung im Kalkspat durch Huyghens [3], die Entdeckung der Aberration (s.d.) des Fixsternlichts durch Bradley (1725), diejenige der dunkeln Linien im Sonnenspektrum durch Wollaston (1802), diejenige der Polarisation des gespiegelten Lichts durch Malus (1809), Fraunhofers Versuche über die dunkeln Linien des Sonnenspektrums (s. [4]) und über die Beugung des Lichts, die definitive Feststellung der Wellentheorie des Lichts durch Th. Young (1802) und Fresnel (1820) [5] und [6], insbesondere des letzteren Interferenzversuch und mathematische Theorie der Doppelbrechung, W. Webers Nachweis des Zusammenhangs der Lichtgeschwindigkeit mit derjenigen der elektrischen Fernwirkung [7], Faradays Versuche über die Drehung der Polarisationsebene des Lichts im magnetischen Felde (1845), die Begründung der Spektralanalyse durch Kirchhoff und Bunsen (1861–63) [8], Maxwells elektromagnetische Lichttheorie [9], experimentelle Begründung der Maxwellschen Theorie durch H. Hertz (1889) [10], die Versuche zur Entscheidung über die Schwingungsrichtung des polarisierten Lichtes mittels stehender Lichtwellen von Wiener [11] und von Drude und Nernst [12].
Die Lehre vom Licht, die Optik, zerfällt in besondere Disziplinen; man unterscheidet die geometrische, physikalische, physiologische Optik, deren erstere sich mit den geometrischen Gesetzen der Strahlung beschäftigt, mit der Geschwindigkeit der Fortpflanzung, der Lichtstärkemessung, der Photometrie, der Spiegelung (Katoptrik), der Brechung (Dioptrik), der Beugung und der Doppelbrechung des Lichtes. Die physikalische Optik setzt die optischen Erscheinungen in Beziehung zu den physikalischen Eigenschaften der Körper und des Aethers, sie behandelt das Licht als Wellenbewegung, die Interferenz, die Farbenzerstreuung, die Absorptions-, Emissions- und Lumineszenzerscheinungen. Soweit sie die Erscheinungen aus letzten einfachen Hypothesen mit Hilfe analytischer Entwicklungen herleitet, heißt sie theoretische oder höhere Optik. Die physiologische Optik beschäftigt sich mit dem Auge als Organ der Licht- und Farbenwahrnehmung, also mit den subjektiven Bedingungen des Unterschieds der Gesichtsempfindungen. Die meteorologische Optik hat die in der Atmosphäre auftretenden, bezw. durch Atmosphärilien veranlaßten Lichterscheinungen zum Gegenstand [31]. Als angewandte Optik bezeichnet man die Lehre vom Gebrauch der optischen Instrumente und der Aufteilung optischer Untersuchungen. Von den am Schlusse dieses Artikels aufgezählten Werken gehören [13]–[16] mehr in das Gebiet der geometrischen Optik, [17]–[23] mehr in das der physikalischen und theoretischen Optik, [24] und [25], sowie größtenteils [13] und [15] sind der Theorie der optischen Instrumente und der angewandten Optik, [26] der physiologischen Optik gewidmet, [27]–[30] haben allgemeinere Tendenz von Kompendien.
Nun folgen hier die wichtigsten Kapitel der geometrischen Optik, während betreffs der wichtigsten Gegenstände der physikalischen, physiologischen und der angewandten Optik auf die besonderen Artikel, wie: Auge, Farbe, Fernrohr, Horopter, Linse, Lumineszenz, Mikroskop, Photometer, Polarisation, Spektralanalyse, Spiegel u.a. verwiesen wird. Hinsichtlich der physikalischen Bedingungen der Lichtaussendung durch Körper vgl. Emission.
II. Geometrische Optik.
Ueber die in verschiedenen Richtungen verschiedene Lichtmenge, welche von der Oberfläche eines leuchtenden Körpers ausstrahlt, gibt das geometrische Strahlungsgesetz von Lambert Auskunft. Die von einem Element der Oberfläche ausgehende Strahlenmenge ist in senkrechter Richtung (Emanationswinkel Null) ein Maximum und in jeder beliebigen Richtung dem Cosinus des Emanationswinkels proportional. Dieses Gesetz ist der Ausdruck der Tatsache, daß ein glühendes ebenes Flächenstück von jeder Richtung her betrachtet gleich hell erscheint, daß z.B. eine glühende Kugel wie eine gleichmäßig helle Scheibe erscheint.
Wie die Mechanik für die Abweichung bewegter Körper von der gleichförmigen Bewegung in gerader Bahn besondere Ursachen voraussetzt, so die Optik für die Abweichung der Strahlen von der Geradlinigkeit. Man unterscheidet drei Arten von Ursachen dieser Abweichung: die Reflexion (Zurückwerfung), die Refraktion (Brechung) und die Inflexion (Beugung).
Reflexion. Bei der Ankunft an der Grenze zweier Mittel spaltet sich die Lichtbewegung in zwei Teile, von denen der eine ins erste Mittel zurückkehrt, reflektiert wird, der andre ins neue Mittel übertritt und entweder hier als gebrochenes Licht sich fortpflanzt oder in eine neue Energieform (Wärme) umgewandelt, d.h. absorbiert wird. Je nachdem die Grenzfläche rauh oder glatt ist, werden die Strahlen diffus, d.h. allseitig von jedem Punkt der Fläche, reflektiert, wie wenn die Fläche selbstleuchtend wäre, oder regelmäßig nach einem Gesetze, das als Reflexionsgesetz bezeichnet wird und die Grundlage der Katoptrik bildet.
Jede glatte, lichtreflektierende Fläche heißt Spiegel. Welches auch die geometrische Gestalt eines Spiegels sei, in seinen kleinsten Flächenelementen ist er eben. Aus dem Grundgesetz des ebenen Spiegels leiten sich daher die Wirkungen andrer Spiegelformen ab. Dieses[152] Grundgesetz selbst ergab sich für die Emissionshypothese als die Folge elastischer Stöße der Lichtteilchen gegen die Spiegelfläche, ergibt sich aber für die Undulationstheorie ebenso als Folge der Reflexion der Wellen an festen Wänden und lautet: der Winkel des einfallenden und des reflektierten Strahls wird vom Einfallslot (Spiegelnormale) halbiert. Das ist das Grundgesetz der Katoptrik; seine Anwendung auf verschiedene Formen des Spiegels s.d.
Eine Fläche, deren Unebenheiten, d.h. Wechsel kleiner Hervorragungen und Vertiefungen an linearer Ausdehnung, nur einen kleinen Bruchteil einer Lichtwellenlänge betragen, wirkt bei der Reflexion als Spiegel; sind die Unebenheiten aber größer als etwa ein Viertel der Wellenlänge, so tritt die diffuse Reflexion auf. Bei sehr schiefer Inzidenz der Strahlen zeigen auch matte Flächen noch Spiegelung. Durch die diffuse Reflexion werden die Körper sichtbar, die kleinsten Teile ihrer Oberfläche wirken wie selbstleuchtend, und zwar nicht in der Farbe des einfallenden Lichtes, sondern in demjenigen Teil dieses Lichtes, das zu dem von der Oberfläche absorbierten Licht komplementär ist. Bei der Bestrahlung durch weißes Licht zeigen daher die Körper eine charakteristische Oberflächenfarbe, bei der Bestrahlung durch farbiges Licht, das die Eigenfarbe eines Körpers nicht enthält, z.B. rote Körper durch grünes Licht, erscheint dieser schwarz.
Wie die Reflexion, so ist auch die Brechung (Refraktion) die Folge physikalischer Ungleichheit des lichtfortpflanzenden Mittels.
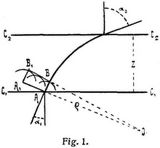
Wenn eine in nichthomogenem Mittel erregte Welle sich fortpflanzt (s. Wellenbewegung), so hat die Geschwindigkeit c der Fortplanzung in verschiedenen Teilen des ungleichartigen Mittels verschiedene Werte. Die Punkte A A1 (Fig. 1) eines ebenen Stücks einer Welle (Punkte, die in übereinstimmender Schwingungsphase begriffen sind) erzeugen Elementarwellen von nicht ganz gleicher Größe, so daß die neue Lage B B1, bis zu der die Welle in dem Zeitteilchen d t fortschreitet, der alten Lage A A1 nicht parallel ist. Kommt der von A ausgehenden Elementarwelle die Geschwindigkeit c, der von A1 ausgehenden die Geschwindigkeit c + d c zu und setzt man A A1 = d n, so schneiden sich die Ebenen A A1 und B B1 derart nach einer Achse O, daß der Strahl A B, d.h. die zur Wellenfläche senkrechte Richtung der Fortpflanzung, um O einen Kreisbogen beschreibt, für dessen Radius wir aus der Proportion:
ρ + d n : ρ = c + d c : c
die Gleichung erhalten:
I. ρ = c : (d c/d n) (Grundgleichung der Refraktion).
Der Quotient dc/dn ist das Gefäll der Fortpflanzungsgeschwindigkeit der Wellen, genommen in Richtung der Normale des gekrümmten Strahls.
Ist eine ebene Schicht von der Dicke z so beschaffen, daß zwischen ihren parallelen Endflächen der Wert c der Wellengeschwindigkeit von c1 bis c2 sich gleichmäßig verändert, so ist g = (c2 – c1)/z das Geschwindigkeitsgefäll der Schicht. Betrachten wir die Schicht als Uebergangsschicht zwischen zwei Mitteln, denen die Werte c1 und c2 zukommen, und macht ein in die Schicht eintretender. Strahl mit der Richtung z (Richtung des Einfallslotes) den Winkel α1 und beim Austritt den Winkel α2 mit derselben Richtung, so ist dc/dn = g sin α und daher ρ = c1 : gsinα1 = c2 : gsinα2, woraus folgt:
II. sin α1/c1 = sin α2/c2 (Sinusgesetz der Refraktion).
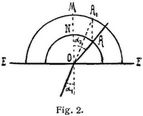
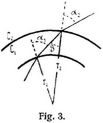
Wird die Dicke z der Schicht zwischen c1 und c2 unendlich klein, d.h. grenzen zwei homogene Schichten mit den Werten c1 und c2 direkt aneinander, so bleibt das Sinusgesetz bestehen, der geradlinige Strahl erleidet an der Grenze zweier Mittel einen Bruch derart, daß der Sinus des Einfallswinkels zum Sinus des Brechungswinkels in konstantem Verhältnis (dem Verhältnis der Werte von c) steht. In dieser Form rührt das Gesetz von Descartes und Snellius her. E. Reusch gibt für die graphische Herleitung der Richtung des gebrochenen aus der des einfallenden Strahls die durch Fig. 2 erläuterte Konstruktion: E E ist die Grenzfläche zweier durchsichtiger Mittel, eines optisch dichteren unten und eines optisch dünneren oben; M O das Einfallslot, A O ein einfallender Strahl, die Verlängerung von A1 O die Richtung des gebrochenen Strahls oder umgekehrt. Die Radien O M und O N der beiden Halbkreise stehen im Verhältnis der Werte von c des oberen und unteren Mittels. – Für eine ganze Reihenfolge paralleler Schichten mit beliebig wechselnden Werten von c folgt aus der Aufeinanderfolge der Gleichungen: sinα1/c1 = sinα2/c2 = sinα3/c3 = u.s.w., daß das Verhältnis sin αn/sinα1 durch das Verhältnis cn/c1 gegeben und von der Beschaffenheit der Zwischenschichten unabhängig ist. Sind die parallelen Schichten nicht eben, sondern sphärisch gekrümmt, so wie z.B. die Luftschichten verschiedener Dichte, welche die Atmosphäre eines Himmelskörpers bilden, so erhält man als Grundgleichung[153] für die Theorie der Strahlenbrechung in konzentrisch geschichteten Mitteln, entsprechend Fig. 3, aus den beiden Gleichungen
folgende Beziehung:
wobei r den Abstand eines Strahlpunkts vom gemeinsamen Kugelmittelpunkt der Schichten, α den jeweiligen Winkel der Strahlrichtung mit der Richtung r bezeichnet. Das Verhältnis der Wellengeschwindigkeit c0 des Lichts im freien Weltraum zu derjenigen c in einem durchsichtigen Mittel heißt der Brechungskoeffizient oder Brechungsindex oder Brechungsexponent des durchsichtigen Mittels; er wird gewöhnlich mit dem Buchstaben n bezeichnet. Nimmt man für das Gefäll von n in Richtung der Normale des gekrümmten Strahls die Bezeichnung n', so lassen sich die obigen drei Gleichungen auf die Formen bringen:
I. ρ = n/n', II. n sin α = Konst., III. n r sin α = Konst.
Eine Zusammenstellung der bis jetzt ermittelten Werte von n bei verschiedenen Substanzen und für verschiedene Farben des Spektrums findet sich in [30]. Einige der wichtigsten Werte, für Farben mittlerer Wellenlänge abgerundet, sind folgende:
Ein an der Grenze zweier Mittel gebrochener Strahl bleibt in der Einfallsebene, der durch den einfallenden Strahl und die Normale der Grenzfläche gelegten Ebene. Ein Bündel Strahlen, die sich im selben Punkt schneiden oder nach demselben Punkt konvergieren, homozentrisches Strahlenbüschel, bleibt bei der Brechung nicht homozentrisch, es wird astigmatisch, die Verlängerungen der Strahlen schneiden sich nach zwei windschiefen zueinander senkrechten Brennlinien. Nur annähernd senkrecht einfallende Strahlenbüschel bleiben homozentrisch und erzeugen bei den optischen Instrumenten gutdefinierte Bilder; s. Astigmatismus.
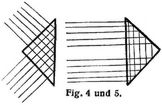
Beim Uebergang des Lichts vom optisch dichteren ins dünnere Mittel, wie von Wasser oder Glas in Luft, findet eine Ablenkung des Strahls vom Einfallslot statt nach der Gleichung sinα2 = n1/n2 sinα1. Da in diesem Fall n1 > n2, so wird α2 > α1. Wenn aber hierbei der Winkel α1, einen gewissen Grenzbetrag überschreitet, so wird sin α2 > 1, der Winkel α2 wird unmöglich. In Fig. 2 läßt sich in solchen Fällen zu Punkt A1 kein Punkt A des inneren Halbkreises finden, weil die Parallele durch A1 zum Einfallslot M O den inneren Halbkreis nicht trifft. Eine an Fig. 1 angeknüpfte Ueberlegung kann darüber Aufschluß geben, welchen Weg der gebrochene Strahl in diesem Falle macht. Der Strahl erreicht die Grenze der Uebergangsschicht nicht, er wendet sich im Bogen zurück zum dichteren Mittel unter demselben Winkel mit dem Einfallslot, wie wenn er gespiegelt worden wäre. Bei unstetigem Wechsel des Wertes von c findet nun aber immer neben der Brechung auch eine Spiegelung statt; es fallen daher bei unmöglichen Werten des Brechungswinkels α2 beide Strahlen, der gebrochene und der gespiegelte, in eine Richtung zusammen: es entsteht die Erscheinung der sogenannten Totalreflexion. Der Grenzwert der möglichen Winkel α2, der sogenannte Grenzwinkel der totalen Reflexion, beträgt entsprechend der Gleichung sin α2 = 1/n (bei Begrenzung der Körper durch Luft oder leeren Raum) für Wasser 48,5°, für Glas 40,8°, für Diamant 23,9°. Je größer der Brechungskoeffizient ist und je stumpfer die Winkel der den Körper begrenzenden Flächen sind (Edelsteinschliff), um so leichter zeigt ein Körper die Erscheinung der Totalreflexion. Sie gestattet, in einem durchsichtigen Wasserstrahl oder in einem gekrümmten Glasstab (Mikroskoplampe) Licht fortzuleiten, wie in einem Rohr mit innen spiegelnden Wänden. Auf ihr beruht die Verwendung des Reflexionsprismas (Fig. 4 und 5), das entweder durch einmalige Totalreflexion an der Hypotenusenfläche eine Strahlablenkung um 90° oder durch zweimalige Totalreflexion an den beiden Kathetenflächen eine Ablenkung um 180° bewirkt. Die erstere Verwendung findet das Reflexionsprisma u.a. bei einigen Distanzmessern, die letztere bei einer Konstruktion des Fernrohrs (Hofmanns Reiterfernrohr), wobei durch eine zweimalige Ablenkung der Strahlen um 180° sowohl eine Aufrechtstellung der im astronomischen Fernrohr umgekehrten Bilder als auch eine Abkürzung der Rohrlänge bewirkt wird. Eine weitere Verwendung der Totalreflexion in Prismen s. bei Camera lucida.
Homogene durchsichtige Körper können trotz der gleichartigen Beschaffenheit aller ihrer Teile noch verschiedenes physikalisches Verhalten in verschiedenen Richtungen zeigen; es kann bei Zug oder Druck der einen Richtung im Körper ein andrer Elastizitätsmodul entsprechen als der andern, es kann in der einen Richtung der Ausdehnungskoeffizient, die Wärmeleitungsfähigkeit anders sein als in einer andern Richtung. Solche Körper heißen anisotrop oder heterotrop, zum Unterschied von den nach allen Richtungen gleichbeschaffenen, den isotropen Körpern. Ihre besonderen optischen Eigenschaften bezeichnet man als Doppelbrechung. Alle Kristalle, soweit sie nicht dem regulären Kristallsystem angehören, sind anisotrop; daraus geschnittene Platten zeigen, mit Ausnahme bestimmter Richtungen des Schnitts, nach zwei aufeinander senkrechten Achsen eine größte und kleinste Wärmeleitungsfähigkeit, wie die schönen Versuche von Sénarmont beweisen. Infolge der Ungleichheit der Ausdehnung je nach der Richtung der Achsen ändern sich auch die Winkel der Kristallflächen beim Erwärmen. Die kristallographischen Hauptachsen sind auch die Achsen der Anisotropie. Als Bild für diese kann man[154] die mit der Richtung veränderliche physikalische Eigenschaft durch die verschiedene Länge der Mittelpunktstrahlen einer um einen Punkt des Innern beschrieben gedachten Fläche, mit drei aufeinander senkrechten Symmetrieebenen darstellen. Diese Fläche, welche in den isotropen Körpern selbstverständlich eine Kugelfläche ist, wird für das hexagonale und quadratische Kristallsystem zur Rotationsfläche, für alle andern Kristallsysteme zu einem dreiachsigen Ellipsoid oder einer diesem verwandten Fläche mit drei zueinander senkrechten ungleichen Achsen.
Auch die Fortpflanzung des Lichtes wird durch die Heterotropie beeinflußt, teils so, daß in den drei Hauptrichtungen die Absorption verschieden ist (s. Dichroismus), teils so, daß die Fortpflanzungsgeschwindigkeit des Lichts je nach der Richtung, in welcher innerhalb eines Kristalls die Lichtschwingungen erfolgen, verschieden ist. Dadurch entstehen die Erscheinungen der Doppelbrechung. Wir wollen ohne analytische Entwicklungen eine geometrische Veranschaulichung der Gesetze geben. Man denke sich zunächst einen langen runden Stab aus Tannenholz, dessen durch die Jahresringe gebildete Schichten alle parallel einem ebenen Achsenschnitt des Stabes gelagert sind. Der Stab zeigt in Richtung der Schichtung einen größeren Widerstand gegen Verbiegung als in dazu senkrechter Richtung. Hätte der Stab rings um die Achse gleiche Verbiegungselastizität, so würde ein gegen das eine Ende in schiefer Richtung geführter Hammerschlag im Stabe zwei Stoßwellen erzeugen, eine Longitudinalwelle oder Verdichtungswelle, welche sich dem Stabe entlang fortpflanzen würde, und eine Transversalwelle oder Verbiegungswelle, welche ebenfalls, aber mit kleinerer Geschwindigkeit als die vorige, sich vom einen zum andern Ende des Stabes fortpflanzen würde. Infolge der verschiedenen Verbiegungselastizität des Stabes spaltet sich nun aber der Schlag im allgemeinen in drei Komponenten und neben der Longitudinalwelle gehen nun dem Stabe entlang zwei Transversalwellen mit zueinander senkrechten Schwingungsrichtungen und ungleichen Geschwindigkeiten, denn nach dem Gesetze (vgl. Wellenbewegung) c = a√e/d worin c die Fortpflanzungsgeschwindigkeit der Welle, e und d die Elastizität und Dichte des Mittels messen, a eine Konstante ist, pflanzt sich die zur Schichtung senkrechte Stoßkomponente langsamer fort als die den Schichten parallele. In den Erscheinungen der Optik treten nun nur Transversalwellen auf; es sind keine Longitudinalwellen, keine Erscheinungen einer Tripelbrechung des Lichts beobachtet. Die periodischen Veränderungen elektrischer bezw. magnetischer Spannung des Lichtäthers, in welchen die Lichtschwingungen bestehen, erfolgen nur in zum Strahl senkrechten Richtungen. Sollten vielleicht die Röntgen- oder die Becquerel-Strahlen longitudinale Aetherwellen darstellen, so haben diese doch keine direkten optischen Wirkungen. Innerhalb eines anisotropen Kristalls hat auch der Lichtäther eine anisotrope Beschaffenheit; es sind im allgemeinen in jeder Richtung durch den Kristall zwei Lichtwellensysteme möglich mit zueinander senkrechten Ebenen der Polarisation (s. Polarisation des Lichts). Nach den Theorien von Fresnel und s. Neumann sind die Lichtschwingungen Elastizitätsschwingungen und die Schwingungsebene entweder senkrecht zur Polarisationsebene oder mit ihr zusammenfallend. Die Einführung dreier Hauptachsen, deren Längen die Quadrate der Elastizitätsmodule messen, führt auf die sogenannte Elastizitätsfläche als Bild des elastischen Verhaltens nach verschiedenen Richtungen. Wir können uns, ohne eine Hypothese über die Schwingungsrichtung zu bevorzugen, des von Cauchy eingeführten Polarisationsellipsoids bedienen, welches zur Elastizitätsfläche in sehr inniger Beziehung fleht. Seine Radien sind bei geeigneter Wahl der entsprechenden Achsen beider Flächen die reziproken Werte der Radien jener Fläche. Zu jeder Strahlrichtung innerhalb des anisotropen Mittels gehören im allgemeinen zwei zueinander senkrechte Richtungen möglicher Polarisation des Strahls, und jeder dieser Polarisationsrichtungen entspricht ein besonderer Wert der Fortpflanzungsgeschwindigkeit entlang dem Strahl.
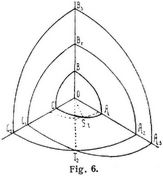
Um einen beliebigen Punkt im Innern eines Kristalls denken wir uns (Fig. 6 zeigt in der Mitte einen Oktanten des Ellipsoids), das Polarisationsellipsoid konstruiert mit den Halbachsen O A = a, O B = b, O C = c, a > b > c, deren Längen denjenigen Geschwindigkeiten umgekehrt proportional sein sollen, mit welchen sich Lichtwellen fortpflanzen, denen diese Achsen als Richtungen der Polarisation der dazu senkrechten Strahlen zugehören. Diese Größen a, b, c sind den Brechungsquotienten der zu ihnen senkrechten und ihrer Richtung parallel polarisierten Strahlen direkt proportional. Die Werte 1/a, 1/b, 1/c sind die Maße der Geschwindigkeiten. In einer gegebenen Zeit t wird sich eine Lichtwelle entlang der Achse O A, wenn sie parallel O B polarisiert ist, um die Weglänge O A2 = t/b fortpflanzen, dagegen um O A3 = t/c, falls sie entlang O C polarisiert ist. Ebenso entsprechen Strahlen in den Richtungen O B und O C als Weglängen in der Zeit t die Längen O B1 und O B3 resp. O C1 und O C2 je nach der Richtung ihrer Polarisation. Für eine beliebige Strahlrichtung von O aus ergeben sich die Weglängen zur Zeit t, wenn man senkrecht zur Strahlrichtung einen ebenen Schnitt durch O legt und in der Schnittellipse die Hauptachsen aufsucht. Die Richtungen und die reziproken Längen dieser Achsen bestimmen die Polarisationsebenen und die Fortpflanzungsgeschwindigkeiten entlang dem Strahl. Auf diese Weise erhält man als Endpunkte der verschiedenen Weglängen die Punkte einer Doppelfläche, der Fresnelschen Wellenfläche, von[155] welcher Fig. 6 ein Bild gibt, indem sie die Schnitte eines Oktanten der Fläche mit den drei Hauptebenen darstellt. Drei der Schnitte sind Kreisquadranten, die andern drei Ellipsenquadranten. Beschreibt man in der Ebene A O C einen Kreis um O mit b, so schneidet dieser die Ellipse AC in vier paarweis diametralen Punkten S1, S2, S'1, S'2. Sowohl der durch O B und S1 S'1 gelegte ebene Schnitt, als der durch O B und S2 S'2 gelegte schneiden das Ellipsoid nach Kreisen. Die beiden zu den Ebenen dieser Kreise senkrechten Strahlen schneiden die Wellenfläche in vier Punkten T1, T2, T'1, T'2, in welchen der innere und äußere Mantel der Wellenfläche ineinander übergehen wie der Mantel eines Kegels und seines Scheitelkegels. Der äußere Mantel ist in den Punkten T trichterförmig vertieft. Die zwei Richtungen O T1 und O T2 heißen die optischen Achsen des Kristalls; entlang diesen Richtungen geht ein Lichtstrahl ohne Spaltung in zwei senkrecht zueinander polarisierte Komponenten durch, die Fortpflanzungsgeschwindigkeit ist für beliebige Richtungen der Polarisation solcher Strahlen dieselbe. – Kommt der Wert der Achsenlängen b entweder dem Werte a oder dem Werte c nahe, so kommt umgekehrt die Richtung der optischen Achsen entweder der Richtung c oder der Richtung a nahe; wird b = a oder b = c, so fallen beide optische Achsen in eine Achse zusammen, die Wellenfläche besteht alsdann aus zwei sich berührenden Flächen, einer Kugel und einem Rotationsellipsoid. Diese Gestalt hat die Wellenfläche in den Kristallen des quadratischen und des hexagonalen Kristallsystems. Diese Kristalle heißen optisch einachsig zum Unterschied von denjenigen Kristallsystemen, deren Symmetrie keine Hauptachse bietet, um welche herum gleiche Gesetzmäßigkeit in verschiedenen Richtungen besteht, den optisch zweiachsigen. Je nachdem bei den einachsigen Kristallen das Ellipsoid die Kugel umschließt (b = c) oder die Kugel das Ellipsoid b = a, wobei in beiden Fällen die Rotationsachse des Ellipsoids Durchmesser der Kugel ist, unterscheidet man negativ einachsige (Kalkspat, Turmalin u.a.) und positiv einachsige (Quarz, Zirkon u.a.).
Für den Uebergang des Lichts aus der Luft oder einem andern isotropen Mittel in ein anisotropisches Mittel erleidet das gewöhnliche Gesetz der Brechung eine wesentliche Veränderung. Während beim Uebergang des Lichtes aus einem isotropen Mittel in ein andres isotropes an der Grenzfläche der Strahl sich in einen reflektierten und einen gebrochenen spaltet, die mit dem einfallenden Strahl und dem Einfallslot in einer Ebene bleiben, so findet an der Grenzfläche eines anisotropen Mittels eine Spaltung in drei Strahlen statt, einen reflektierten und zwei gebrochene, beide letztere wegen der verschiedenen Brechungsquotienten von verschiedener Richtung und im allgemeinen der eine oder beide aus der Einfallsebene heraustretend.
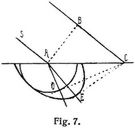
Fig. 7 zeigt um einen Punkt der Schnittfläche eines zerschnittenen Kalkspatkristalls die ins Innere des Kristalls fallende Hälfte der Wellenfläche bezw. deren Schnitt mit der Einfallsebene konstruiert, diese Fläche in solcher Ausdehnung, daß in derselben Zeit t, in welcher eine ebene Lichtwelle A B in der Luft die Weglänge B C zurücklegen würde, die beiden von A aus sich im Kristall ausbreitenden Wellen an die Oberfläche der Wellenfläche gelangen. Nach der Zeit t bilden sich aus der ebenen Welle A B in der Luft die ebenen Wellen C E und C O im Kristall, denen als Strahlrichtungen in der Luft der Strahl S A, im Kristall die Strahlen A E und A O entsprechen. Die Punkte E und O erhält man, wenn man durch C senkrecht zur Einfallsebene (Zeichnungsebene) Berührungsebenen an die zwei Teile der Wellenfläche legt, an die Kugel und das Ellipsoid. Der Strahl A O folgt den Gesetzen der gewöhnlichen Brechung, er liegt immer in der Einfallsebene, er heißt der ordinär gebrochene Strahl. Nicht so der Strahl O E. Der Berührungspunkt E fällt nur dann in die Einfallsebene, wenn auch die Hauptachse der Wellenfläche in der Einfallsebene liegt, die Hauptachse des Kristalls der Einfallsebene parallel ist. Der Strahl O E heißt der extraordinäre Strahl. Bei den zweiachsigen Kristallen sind beide Strahlen extraordinär gebrochen, da im allgemeinen beide von C an die Wellenfläche gelegte Berührungsebenen Berührungspunkte außerhalb der Einfallsebene ergeben. In einem ganz besonderen Fall entstehen sogar mehr als zwei gebrochene Strahlen, dann nämlich, wenn die von C aus gelegte Berührungsebene die Wellenfläche rings um den Punkt T (Fig. 6) nach einem geschlossenen Kreise berührt; der von A ausgehende Strahl spaltet sich dann in einen Strahlenkegel, es ist das der Fall der konischen Refraktion, welche von Hamilton theoretisch gefolgert, von Lloyd experimentell nachgewiesen wurde.
Infolge der Spaltung des in ein doppelbrechendes Mittel eintretenden Strahls in zwei Strahlen verschiedener Richtung zeigen diese Mittel doppelte Bilder der durch sie gesehenen Objekte. Bei planparallelen Platten werden die Strahlen beim Austritt wieder parallel; der Abstand zweier zusammengehöriger Strahlen ist daher der Plattendicke proportional. Bei Prismen dagegen verladen die zusammengehöriger Strahlen die Austrittsfläche in divergenten Richtungen. Rochons Prisma, durch Verbindung zweier Prismen mit zueinander senkrechten Richtungen der optischen Achse achromatisch gemacht, dient, zwischen Objektiv und Bildebene eines Fernrohrs eingeschaltet, als Mikrometer und als Distanzmesser. Je mehr innerhalb des Rohrs das Prisma gegen das Objektiv verschoben wird, um so weiter treten im Sehfeld die zwei Bilder eines Punktes auseinander.
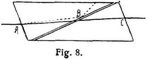
Die Doppelbrechung bietet bequeme Mittel zur Herstellung von Polarisatoren und Analysatoren der Polarisationsapparate (s. Polarisation des Lichts). In dem Nicolschen Prisma (Fig. 8) ist ein Kalkspatkristall derart schief durchschnitten und sind die zu den durchgehenden Strahlen schiefen Schnittflächen unter Zwischenbringen einer Schicht einer schwächer brechenden Substanz (Kanadabalsam, Luft) einander wieder genähert, daß die[156] stärker gebrochenen ordinären Strahlen (Strahl A B der Figur) an der Zwischenschicht eine totale Reflexion erfahren, die extraordinären Strahlen (Strahl A C), aus dem Prisma austretend, eben polarisiertes Licht liefern. Polarisiertes Licht, welches durch das Prisma geleitet wird, geht durch, wenn die Polarisationsebene mit derjenigen des extraordinären Strahls übereinstimmt, nicht aber, wenn sie diejenige des ordinären Strahls ist. Beim Drehen des Nikols um den Strahl als Achse erhält man mit polarisiertem Lichte abwechselnd helles und dunkles Feld. Eine Platte aus schwarzem Turmalin, entlang der Kristallachse geschliffen, liefert ohne weiteres polarisiertes Licht, da sie den einen der beiden Strahlen absorbiert; in der Turmalinzange zeigen die parallel gestellten Platten helles, die gekreuzten Platten dunkles Gesichtsfeld.
Nicht bloß Kristalle, auch amorphe Körper können anisotrop sein und Erscheinungen der Doppelbrechung zeigen, wie z.B. Gläser, wenn sie in der einen Richtung gepreßt werden oder wenn sie einer ungleichmäßigen Abkühlung unterworfen wurden. Der Zustand dielektrischer Polarisation in einem elektrischen Felde ändert das optische Verhalten der doppelbrechenden Kristalle und gibt Flüssigkeiten die Eigenschaft einachsiger Kristalle. Der Doppelbrechung unterliegen nicht nur die Strahlen bezw. Wellen des Lichts, sondern auch diejenigen der Wärme, die elektrischen Wellen der Hertzschen Versuche und selbst die Stoßwellen der Erdbeben, welche im Innern der Erdkruste vielleicht gar eine Tripelbrechung erfahren, nicht aber die Wellen des Schalls, weil diese als Verdichtungs- und Verdünnungswellen nicht durch Transversal-, sondern durch Longitudinalschwingungen gebildet werden.
Beugung (Inflexion, Diffraktion) des Lichtes heißt die Ablenkung von der geradlinigen Fortpflanzung, die das Licht am Rande undurchsichtiger Körper erfährt. Die Beugungserscheinungen sind Wirkungen dieser Ablenkung und der Interferenz des Lichtes.
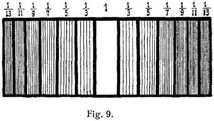
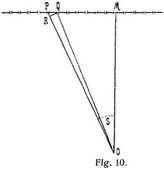
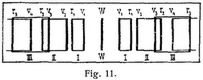
Trifft ein schmales Bündel paralleler Lichtstrahlen auf einen engen Spalt und dringt es durch diesen in eine Dunkelkammer (Camera obscura), so erzeugt es auf der dem Spalt gegenüberstehenden Wand nicht bloß ein direktes Bild des Spaltes, sondern, falls man mit einfarbigem Lichte experimentiert, eine größere Anzahl schwächerer Bilder zu beiden Seiten des Hauptbildes (Fig. 9) von einer mit wechselnder Entfernung vom Hauptbilde abnehmenden Intensität. Falls man weißes Licht hat, zeigt sich das Hauptbild zu beiden Seiten durch Streifen prismatischer Farben umsäumt (Interferenzfransen) Bei der Fortpflanzung von Wellen in irgendwelchem Mittel bildet nämlich jeder Punkt, der von der Wellenbewegung ergriffen wird, wieder den Ausgangspunkt neuer Wellen, der sogenannten Elementarwellen (s. Wellenbewegung), durch deren Zusammenwirken (Interferenz) eben die Hauptwellen entstehen. Von allen Punkten des Spaltes gehen nach allen Richtungen Elementarwellen ins Innere der Kammer. Am Orte des mittleren Hauptbildes treffen alle diese Wellen gleichzeitig mit gleicher Schwingungsphase ein. Zu beiden Seiten des Hauptbildes aber werden die Wege der Lichtstrahlen, die vom rechten oder linken Rande des Spaltes ausgehen, ungleich. Beträgt die Differenz der Wege eine Lichtwellenlänge λ, so entsteht am betreffenden Orte Dunkel, denn die von der einen Hälfte der Spaltbreite kommenden Wellen interferieren mit denen der andern Hälfte wegen der Wegdifferenz von 1/2λ zwischen je zweien derselben derart, daß sie sich gegenseitig vernichten. Beträgt aber die Wegdifferenz zwischen den von den Rändern kommenden Wellen 11/2λ, so erhält man wieder Hell, weil nur zwei Drittel der Spaltbreite durch Interferenz unwirksam werden. Die Lichtintensität dieses ersten Bildpaares zu beiden Seiten des Hauptbildes ist nur ein Drittel der Intensität des Hauptbildes. Bei 2λ Differenz erfolgt wieder Dunkel, denn die ganze Spaltbreite läßt sich in vier Teile teilen, von denen der zweite die Wirkung des ersten, der vierte die Wirkung des dritten aufhebt. Bei der Differenz 21/2λ entsteht das zweite Bildpaar mit einem Fünftel Intensität u.s.w. Da für Licht verschiedener Farbe λ verschiedene Werte hat, so ist die Entfernung der blauen Bilder voneinander kleiner als diejenige z.B. grüner oder gelber Bilder, und die Entfernungen dieser Bilder sind kleiner als diejenigen des Rot. Je weiter man sich aber von dem mittleren Bilde entfernt, in um so mannigfaltigerer Weise überdecken sich die farbigen Erscheinungen und verschwinden. Von besonderer Schönheit sind die Gittererscheinungen – Beugungserscheinungen, die aus dem Zusammenwirken sehr vieler benachbarter paralleler Spalten in kleinen regelmäßigen Abständen voneinander entstehen. Die Drahtgitter, seine parallele Drähte in geringen gleichen Abständen, Rußgitter, parallele mit einer Nadel auf berußtem Glas gezogene Linien, zarte Vogelfedern mit ihren parallelen Fäserchen, besonders aber die Glasgitter, mit der Teilmaschine und einer Diamantspitze auf Glas aufgetragene, feinste parallele Linien, zeigen beim Durchsehen nach einem fernen Lichtpunkt sehr schöne prismatische Erscheinungen. In größter Feinheit (14000 Linien auf den Zoll engl.) wurden die Gitter von Rowland hergestellt und noch auf photographischem Wege verjüngt (Rowlands Konkavgitter). Diese dienen zur Erzeugung der reinsten Spektren des Sonnenlichts und zeigen die Fraunhoferschen Linien. Da bei dieser Erzeugung des Spektrums zum Unterschiede von der Erzeugung durch Brechung in[157] Prismen (Brechung) der Ort der Linien nur von der Teilung des Gitters und der Wellenlänge abhängt, so gestattet sie die schärfste Feststellung der Wellenlängen. Zur kurzen Erklärung der Entstehung des Spektrums durch Gitter mögen die Fig. 10 und 11 dienen: Das Auge O steht durch ein vorgehaltenes Gitter in der Richtung O M nach einem fernen Lichtpunkte, die von zwei Nachbarspalten P und Q im Abstande P Q = d ausgehenden Elementarwellen besitzen einen Gangunterschied O P – O Q = P R = dsinφ. Beträgt dieser Gangunterschied eine ganze Wellenlänge λ oder 2λ oder 3λ, so erhält das Auge in der Richtung des Winkels φ Hell, da in dieser Richtung sich die Einzelwellen summieren. Ist aber d sin φ = λ/2, so entsteht Dunkel, weil sich die Elementarwellen durch Interferenz aufheben. Ebenso bei d sin φ = 3λ/2 oder 5λ/2 u.s.w. Aber auch bei d sin φ = λ/4 oder 3λ/4 weiteren Zwischenabteilungen wird Dunkel entstehen, weil in der Richtung φ jeder Strahl durch Interferenz mit dem übernächsten unwirksam wird. Eine bestimmte Farbe, z.B. Rot, wird daher neben dem direkten Bilde W (Fig. 11) in denjenigen Richtungen φ seitliche Bilder r1, r2, r3 u.s.w. erzeugen, in denen die Gangunterschiede λ, 2λ, 3λ des roten Lichtes betragen. Eine andre Farbe, z.B. Violett, das, am andern Ende des Spektrums liegend, eine nur stark halb so große Wellenlänge hat, erzeugt seitliche Bilder v1, v2, v3 u.s.w. in kleineren Abständen von W. So entsteht durch das weiße Licht einer fernen Spalte zu beiden Seiten des weißen Bildes W ein System von Spektren I, II, III u.s.w., deren erstes von den übrigen getrennt fleht, deren folgende sich mehr und mehr überdecken und gemischte Farbeneindrücke erzeugen. Nicht bloß im durchgehenden Lichte, auch bei Reflexion zeigen die Gitter solche farbige Erscheinungen. Die Perlmutter verdankt ihr Farbenspiel einer seinen Streifung, die man durch Abdrücken auf Guttapercha samt dem Farbenspiel übertragen kann. Die Bartonschen Irisknöpfe sind durch Gravierung mit gestreifter Oberfläche versehene Metallknöpfe. Fraunhofer hat experimentell gezeigt, daß kleine Körperchen von annähernd gleicher Größe (Bärlappsamen auf einer Glasplatte) im zwischen ihnen durchgehenden Licht einer Flamme, der Sonne, des Mondes ebenfalls Beugungserscheinungen liefern, wodurch die kleinen Höfe um Sonne und Mond sich erklären, Systeme farbiger Ringe mit um so größeren Durchmessern, je kleiner die erzeugenden Dunstkörperchen sind. Auch der sogenannte Heiligenschein, die Aureole um den Schatten des Kopfes auf betauter Wiese, der Ring des Ulloa, eine Ringbildung um den Kopf beim Brockengespenst sind solche Beugungserscheinungen, nur nicht im durchgehenden, sondern im zurückgeworfenen Lichte erzeugte. Von technischem Interesse ist die Möglichkeit, auf der Oberfläche von Glaswaren eine seine kristallinische Absonderung zu erzeugen und sie dadurch farbig schillernd zu machen, indem man im Ofen bei hoher Temperatur Salzsäuredämpfe auf dieselben einwirken läßt.
Literatur: [1] Kepler, Opera omnia, ed. Frisch, II, S. 530, Frankfurt-Erlangen 1858–71. – [2] Descartes, Essais philosophiques, Leyden 1637. – [3] Huyghens, Traité de la lumière, Leyden 1690. – [4] Fraunhofer, Bestimmungen des Brechungs- und Farbenzerstreuungsvermögens u.s.w., Denkschr. d. Münchener Akad. 1814–15. – [5] Course of lectures of natural philosophy, London 1845. – [6] Œuvres complètes d'Aug. Fresnel, Paris 1866–70. – [7] Elektrodynam. Maßbestimmungen, Abhandl. d. Sächs. Akad. d. Wissensch. 1846. – [8] Chemische Analyse durch Spektralbeobachtungen, G. Kirchhoff, Gesammelte Abhandlungen, Leipzig 1882. – [9] Maxwell, A treatise on electricity and magnetism, Oxford 1873. – [10] Hertz, H., Gesammelte Werke, Leipzig 1894. – [11] Wiener, O., Stehende Lichtwellen u.s.w., Wied. Ann. 40, 1890, S. 203. – [12] Drude und Nernst, Ueber die Fluoreszenzwirkungen stehender Lichtwellen, Wied. Ann. 46, 1892, S. 460. – [13] Ferraris, G., Le proprietà cardinali degli istrumenti diottrici, esposizione elementare della teoria di Gauss, Turin 1877, deutsch von Lippich, Leipzig 1879. – [14] Meisel, Geometrische Optik, Halle 1886. – [15] Czapski, Theorie der optischen Instrumente, Breslau 1893, 2. Aufl., Leipzig 1904. – [16] Heath, Lehrbuch der geometrischen Optik, deutsch von Harnak, Berlin 1894. – [17] Airy, G.B., On the undulatory theory of optics, neue Ausgabe, Cambridge 1877 (mathemat. tracts, 4. Aufl.). – [18] Beer, A., Einleitung in die höhere Optik, 2. Aufl., bearbeitet von V. v. Lang, Braunschweig 1882. – [19] Billet, Traité d'optique physique, Paris 1850–59. – [20] Neumann, J., Vorlesungen über theoretische Optik, herausgegeben von F. Dorn, Leipzig 1885. – [21] Verdet, E., Leçons d'optique physique, publiées par Levistal, Paris 1869–70, deutsch: Exner, Vorlesungen über die Wellentheorie des Lichts, 2 Bde., Braunschweig 1881–87. – [22] Kirchhoff, Vorlesungen über mathemat. Optik, Leipzig 1891. – [23] Helmholtz, H. v., Vorlesungen über die elektromagnetische Theorie des Lichts, herausgegeben von A. König und C. Runge, Hamburg und Leipzig 1897. – [24] Littrow, J., Dioptrik oder Anleitung zur Verfertigung von Fernrohren, Wien 1830. – [25] Steinheil und Voit, Handbuch der angewandten Optik, Leipzig 1890. – [26] Helmholtz, H. v., Handbuch der physiologischen Optik, 2. Aufl., Hamburg 1886. – [27] Radicke, G., Handbuch der Optik, 2 Bde., Berlin 1839. – [28] Moigno, N., Répertoire d'optique moderne, 4 Bde., Paris 1847–50. – [29] Mascart, M., Traité d'optique, Bd. 1, Paris 1889. – [30] Winkelmann, Handbuch der Physik, Bd. 2, 1, Optik, Breslau 1894, und 2. Aufl., Bd. 6, zweite Hälfte, Leipzig 1906. – [31] Pernier, J.M., Meteorologische Optik, Wien und Leipzig 1902–06.
Aug. Schmidt.
Adelung-1793: Licht, das · Licht · -Licht
Brockhaus-1911: Licht [3] · Monochromatisches Licht · Zerstreutes Licht · Licht [2] · Elektrisches Licht · Ewiges Licht · Licht
DamenConvLex-1834: Schatten und Licht · Licht
Eisler-1904: Natürliches Licht · Licht und Finsternis
Herder-1854: Licht · Galvanisches Licht · Ewiges Licht
Lueger-1904: Licht [4] · Licht [3] · Moore-Licht · Ultraviolettes Licht [2] · Ultraviolettes Licht [1] · Licht [2] · Ankerlaterne, -licht · Ankerkran-, -laterne, -licht · Drummondsches Licht · Licht und Luft · Dufton-Gardner-Licht
Meyers-1905: Licht, philosophisches · Licht [2] · Licht [1] · Licht, schwarzes · Philosophisches Licht · Monochromatisches Licht · Licht. · Drummondsches Licht · Ausstrahlung von Wärme, Licht und chemischen Strahlen · Auersches Licht · Elektrisches Licht · Inneres Licht · Falsches Licht · Ewiges Licht
Pierer-1857: Licht im Schatten · Licht u. Recht · Falsches Licht · Abgedämpftes Licht · Drummondsches Licht
Buchempfehlung
Holz, Arno
Die Familie Selicke
Das bahnbrechende Stück für das naturalistische Drama soll den Zuschauer »in ein Stück Leben wie durch ein Fenster« blicken lassen. Arno Holz, der »die Familie Selicke« 1889 gemeinsam mit seinem Freund Johannes Schlaf geschrieben hat, beschreibt konsequent naturalistisch, durchgehend im Dialekt der Nordberliner Arbeiterviertel, der Holz aus eigener Erfahrung sehr vertraut ist, einen Weihnachtsabend der 1890er Jahre im kleinbürgerlich-proletarischen Milieu.
58 Seiten, 4.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Romantische Geschichten II. Zehn Erzählungen
Romantik! Das ist auch – aber eben nicht nur – eine Epoche. Wenn wir heute etwas romantisch finden oder nennen, schwingt darin die Sehnsucht und die Leidenschaft der jungen Autoren, die seit dem Ausklang des 18. Jahrhundert ihre Gefühlswelt gegen die von der Aufklärung geforderte Vernunft verteidigt haben. So sind vor 200 Jahren wundervolle Erzählungen entstanden. Sie handeln von der Suche nach einer verlorengegangenen Welt des Wunderbaren, sind melancholisch oder mythisch oder märchenhaft, jedenfalls aber romantisch - damals wie heute. Michael Holzinger hat für den zweiten Band eine weitere Sammlung von zehn romantischen Meistererzählungen zusammengestellt.
- Novalis Die Lehrlinge zu Sais
- Adelbert von Chamisso Adelberts Fabel
- Jean Paul Des Feldpredigers Schmelzle Reise nach Flätz
- Clemens Brentano Aus der Chronika eines fahrenden Schülers
- Friedrich de la Motte Fouqué Eine Geschichte vom Galgenmännlein
- E. T. A. Hoffmann Der goldne Topf
- Joseph von Eichendorff Das Marmorbild
- Ludwig Achim von Arnim Die Majoratsherren
- Ludwig Tieck Die Gemälde
- Wilhelm Hauff Die Bettlerin vom Pont des Arts
428 Seiten, 16.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum